Introduction to Graph Theory
Notes from the book Discrete Mathematics with Application (Kenneth H. Rosen)
Graph and Graph models
A graph $G=(V,E)$ consists of $V$, an nonempty set of vertices (or nodes) and $E$, a set of edges. Each edge has either one or two vertices associated with it, called its endpoints. An edge is said to connect its endpoints.
A graph with infinite vertex or egdes is called infinite graph. In the otherwise case, finite graph.
A graph in which each edge connects two different vertices and where no two edges connect the same pair of vertices is called a simple graph.
Graph that may have multiple edges connecting the same vertices are called multigraphs.
The edges that connect a vertex to itself are called loops.
Graphs including loops, and possibly multiple edges connecting the same pair of vertices or a vertex to itself, are called pseudographs.
The graph with undirected edges is an undirected graph.
A directed graph (or digraph) $(V,E)$ consists of a nonempty set of vertices $V$ and a set of directed edges (or arcs) $E$. Each directed edge is associated with an ordered pair of vertices. The directed edge associated with the ordered pair $(u,v)$ is said to start at $u$ and end at $v$.
A directed graph has no loops and has no multiple directed edges is called a simple directed graph.
Directed graphs that may have multiple directed edges from a vertex to a second (possibly the same) vertex are used to model such networks are called directed multigraphs. When there are $m$ directed edges, each associated to an ordered pair of vertices $(u,v)$, we say that $(u,v)$ is an edge of multiplicity $m$.
A graph with both directed and undirected edges is called a mixed graph.
Graphs are used in a wide variety of models:
- Social networks
- Communication networks
- Information networks
- Software design applications
- Transportation networks
- Biological networks
- Tournaments
Terminology and special types of graph
Terminology
Two vertices u and v in an undirected graph G are called adjacent (or neighbors) in G if u and v are endpoints of an edge e of G. Such an edge e is called incident with the vertices u and v and e is said to connect u and v.
The set of all neighbors of a vertex v of $G=(V,E)$, denoted by $N(v)$, is called the neighborhood of $v$. If $A$ is a subset of $V$ , we denote by $N(A)$ the set of all vertices in $G$ that are adjacent to at least one vertex in A. So, $N(A)=\bigcup_{v\in A}N(v)$.
The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. The degree of the vertex v is denoted by $deg(v)$.
A vertex of degree zero is called isolated (not adjacent to any vertex).
A vertex is pendant if and only if it has degree one (adjacent to exactly one other vertex).
Let $G=(V,E)$ be an undirected graph with $m$ edges: $$2m=\sum_{v\in V}\deg(v)$$
This theorem shows that the sum of the degrees of the vertices of an undirected graph is even, which lead to the below theorem.
When $(u,v)$ is an edge of the graph G with directed edges, $u$ is said to be adjacent to $v$ and $v$ is said to be adjacent from $u$. The vertex $u$ is called the initial vertex of $(u,v)$, and $v$ is called the terminal or end vertex of $(u,v)$. The initial vertex and terminal vertex of a loop are the same.
In a graph with directed edges the in-degree of a vertex v, denoted by $\deg^{-}(v)$, is the number of edges with v as their terminal vertex. The out-degree of v, denoted by $\deg^{+}(v)$, is the number of edges with v as their initial vertex. (Note that a loop at a vertex contributes 1 to both the in-degree and the out-degree of this vertex.)
Some special simple graphs:
- Complete Graphs: a complete graph on n vertices, denoted by $K_{n}$, is a simple graph that contains exactly one edge between each pair of distinct vertices.
- Wheels
- n-cube / n-dimensional hypercube, denoted by $Q_{n}$, is a graph that has vertices representing the $2^{n}$ bit strings of length n.
Bipartite Graph
A simple graph $G$ is called bipartite if its vertex set $V$ can be partitioned into two disjoint sets $V_{1}$ and $V_{2}$ such that every edge in the graph connects a vertex in $V_{1}$ and a vertex in $V_{2}$ (so that no edge in $G$ connects either two vertices in $V_{1}$ or two vertices in $V_{2}$). When this condition holds, we call the pair $(V_{1},V_{2})$ a bipartition of the vertex set $V$ of $G$.
A complete bipartite graph $K_{m,n}$ is a graph that has its vertex set partitioned into two subsets of $m$ and $n$ vertices, respectively with an edge between two vertices if and only if one vertex is in the first subset and the other vertex is in the second subset.
A matching $M$ in a simple graph $G=(V,E)$ is a subset of the set $E$ of edges of the graph such that no two edges are incident with the same vertex. In other words, a matching is a subset of edges such that if ${s,t}$ and ${u,v}$ are distinct edges of the matching, then s, t, u, and v are distinct.
A vertex that is the endpoint of an edge of a matching $M$ is said to be matched in $M$; otherwise it is said to be unmatched.
A maximum matching is a matching with the largest number of edges. We say that a matching M in a bipartite graph $G=(V,E)$ with bipartition $(V_{1},V_{2})$ is a complete matching from $V_{1}$ to $V_{2}$ if every vertex in $V_{1}$ is the endpoint of an edge in the matching, or equivalently, if $|M|=|V_1|$.
The bipartite graph $G=(V,E)$ with bipartition $(V_{1},V_{2})$ has a complete matching from $V_{1}$ to $V_{2}$ if and only if $\|N(A)\| \ge \|A\|$ for all subsets A of $V_{1}$.
Representing Graphs and Graph Isomorphism
Adjacency Lists
One way to represent a graph without multiple edges is to list all the edges of this graph. Another way to represent a graph with no multiple edges is to use adjacency lists, which specify the vertices that are adjacent to each vertex of the graph.

Adjacency Matrices
Suppose that $G = (V , E)$ is a simple graph where $|V| = n$. Suppose that the vertices of $G$ are listed arbitrarily as $v_1, v_2, …, v_n$ .
The adjacency matrix $A$ (or $A_G$ ) of $G$, with respect to this listing of the vertices, is the $n \times n$ zero–one matrix with 1 as its $(i, j)$th entry when $v_i$ and $v_j$ are adjacent, and 0 as its $(i,j)$th entry when they are not adjacent.
In other words, if its adjacency matrix is $A = [a_{ij}]$, then
\[a_{ij} = \left\{ \begin{matrix} 1 & \text{if } {v_i, v_j} \text{ is an edge of G} \\ 0 & \text{otherwise} \end{matrix} \right.\]
Incidence Matrices
Let $G = (V , E)$ be an undirected graph. Suppose that $v_1 , v_2 , . . . , v_n$ are the vertices and $e1 , e2 , . . . , e_m$ are the edges of G. Then the incidence matrix with respect to this ordering of $V$ and $E$ is the $n \times m$ matrix $M = [m_{ij}]$, where
\[m_{ij} = \left\{ \begin{matrix} 1 & \text{when edge } e_j \text{ is incident with } v_i \\ 0 & \text{otherwise} \end{matrix} \right.\]
Isomorphism
In other words, when two simple graphs are isomorphic, there is a one-to-one correspondence between vertices of the two graphs that preserves the adjacency relationship. Isomorphism of simple graphs is an equivalence relation.
A property preserved by isomorphism of graphs is called a graph invariant. For example, isomorpic graphs must have:
- The same # of vertices
- The same # of edges
- The degrees of the vertices in the graphs must be the same
Connectivity
Paths
A path of length $n$ from $u$ to $v$ in $G$ is a sequence of $n$ edges $e_1,...,e_n$ of $G$ for which there exists a sequence $x_0 = u,x_1,\dots,x_{n−1},x_n = v$ of vertices such that $e_i$ has, for $i = 1,\dots,n$, the endpoints $x_{i−1}$ and $x_i$.
When the graph is simple, we denote this path by its vertex sequence $x_0,x_1,\dots,x_n$ (because listing these vertices uniquely determines the path).
The path is a circuit if it begins and ends at the same vertex, that is, if u = v, and has length greater than zero.
The path or circuit is said to pass through the vertices $x_1, x_2,\dots, x_{n−1}$ or traverse the edges $e_1, e_2,\dots, e_n$. A path or circuit is simple if it does not contain the same edge more than once.
Read more: Erdős Number, Bacon number.
Connectedness in Undirected Graphs
An undirected graph that is not connected is called disconnected.
We say that we disconnect a graph when we remove vertices or edges, or both, to produce a disconnected subgraph.
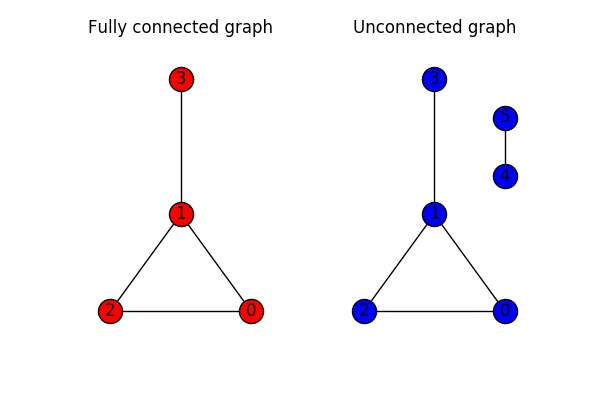
That is, a connected component of a graph G is a maximal connected subgraph of G.
A graph G that is not connected has two or more connected components that are disjoint and have G as their union.

Read more: Finding Connected Components using DFS
How Connected is a Graph?
An edge whose removal produces a graph with more connected components than in the original graph is called a Cut edge or Bridge.
(javatpoint)
Vertex Connectivity
When a complete graph $K_n$ removes a vertex and all incidents to it, the resulting graph is a complete graph $K_{n-1}$ which also a connected graph.
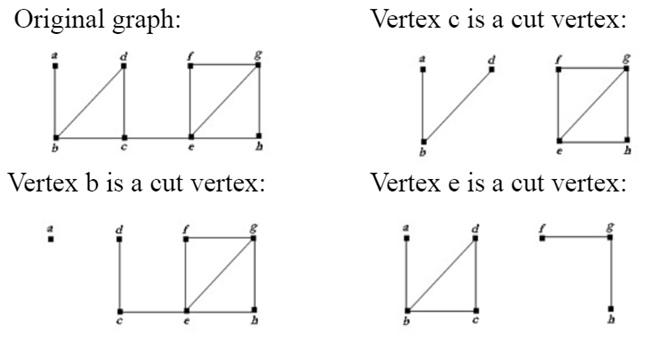
Connected graph having no cut vertex is a nonseparable graph which is more connected than a graph with a cut vertex.
A subset $V'$ of the vertex set $V$ of $G=(V,E)$ is a vertex cut, or separating set, if $G-V'$ is disconnected.
Vertex connectivity of a noncomplete graph $G$, denoted by $\kappa(G)$, is the minimum number of vertices in a vertex cut.

(stackexchange)
When $G$ is a complete graph, it has no vertex cuts. Because removing any vertex and its incident edges still leaves a complete graph.
So, it’s impossible to define $\kappa(G)$ as the smallest number of vertices in a vertex cut when $G$ is complete. In this case, we define $\kappa(K_n) = n-1$ as the number of vertices needed to be removed to produce a graph with a single vertex.
In conclusion, for every graph G, $\kappa(G)$ is the minimum number of verties that can be removed from graph to either:
- Disconnect G or
- Prduce a graph with a single vertex
We have:
- $0 \le \kappa(G) \le n-1$ if G has n vertices
- $\kappa(G) = 0$ if and only if G is disconnected or $G = K_1$
- $\kappa(G) = 1$ if and only if G is complete
The larger k(G) is, the more connected G is:
- Disconnected graph or $K_1$ have $\kappa(G) = 0$
- Connected graph with cut vetices and $K_2$ have $\kappa(G) = 1$
- Graph without cut vertices and $K_3$ have $\kappa(G) = 2$
- so on …
A graph is k-connected or k-vertex-connected if $\kappa(G) \ge k$:
- 1-connected graph if it is connected and not a graph containing a single vertex
- 2-connected is also called biconnected that is non seperable and has at least three vertices
- G is a k-connected graph, then G is a j-connected for all j with $0 \le j \le k$
Edge Connectivity
A set of edge E' is called an edge cut of G if the subgraph $G - E'$ is disconnected.
The edge connectivity of a graph G, denoted $\lambda(G)$, is the minimum number of edges in an edge cut of G.
We always define $\lambda(G)$ for any connected graphs with at least one vertex because it is always possible to disconnect a graph by removing all edges incident to one of its vertices.
- $\lambda(G) = 0$ if G is not connected.
- If G is a graph with $n$ vertices, then $0 \le \lambda(G) \le n - 1$
- $\lambda(G) = n - 1$ if and only if $G = K_n$
- $\lambda(G) \le n - 2$ if and only if G is not a complete graph.
Read more:
Connectedness in Directed Graphs
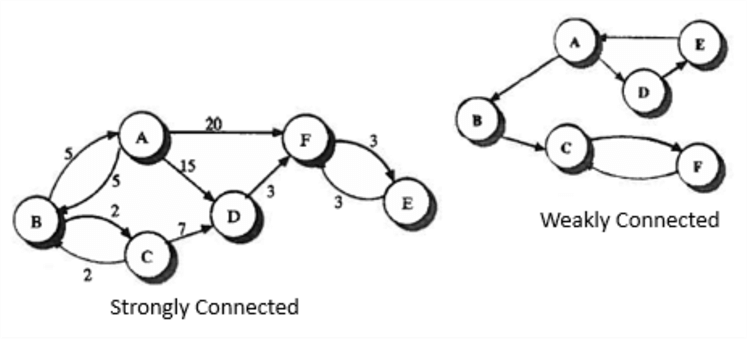
A directed graph is strongly connected if there is a path from a to b and from b to a whenever a and b are vertices in the graph.
A directed graph is weakly connected if there is a path between every two vertices in the underlying undirected graph.
A directed graph is weakly connected if and only if there is always a path between two vertices when the directions of the edges are disregarded. Clearly, any strongly connected directed graph is also weakly connected.
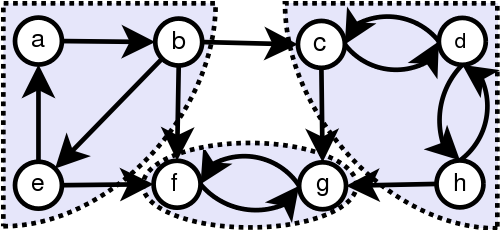
Read more:
Paths and Isomorphism
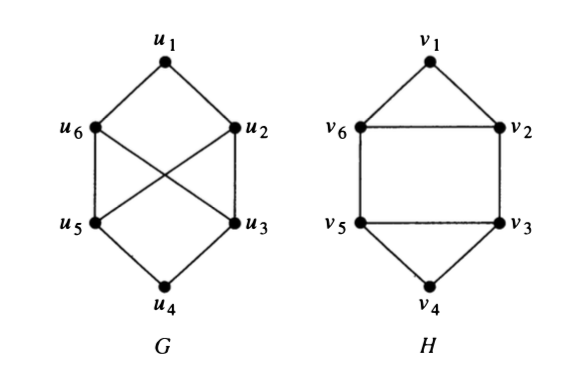
Both $G$ and $H$ have same three invariants: number of vertices, number of edges, and degrees of vertices—all agree for the two graphs.
However, $H$ has a simple circuit of length three, namely, $v_1, v_2, v_6, v_1$, whereas $G$ has no simple circuit of length three, as can be determined by inspection (all simple circuits in $G$ have length at least four). Because the existence of a simple circuit of length three is an isomorphic invariant, $G$ and $H$ are not isomorphic.
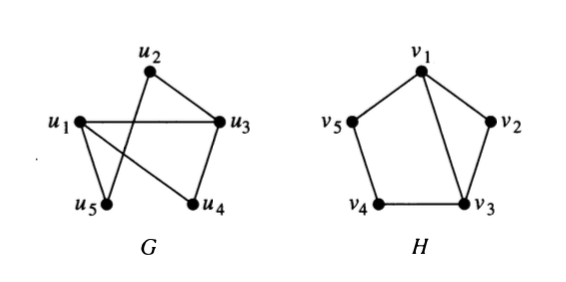
Both G and H have five vertices and six edges, both have two vertices of degree three and three vertices of degree two, and both have a simple circuit of length three, a simple circuit of length four, and a simple circuit of length five. Because all these isomorphic invariants agree, G and H may be isomorphic.
To confirm isomorphism, find the path go through all same degrees of 2 graphs. For example, the paths $u_1 \rightarrow u_4 \rightarrow u_3 \rightarrow u_2 \rightarrow u_5$ in $G$ and $v_3 \rightarrow v_2 \rightarrow v_1 \rightarrow v_5 \rightarrow v_4$ in $H$ both go through degrees: $3 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 2$. So, we can establish a mapping $f$ with $f(u_1) = v_3$, $f(u_4) = v_2$, $f(u_3) = v_1$, $f(u_2) = v_5$, and $f(u_5) = v_4$, this leads to that $G$ and $H$ are isomorphic.
Counting Paths Between Vertices
The number of different paths of length $r$ from $v_i$ to $v_j$, where $r$ is a positive integer, equals the $(i, j)$th entry of $A^r$.
For example (sfu):
The graph :
Adjacency Matrix:
\[M=\left[\begin{smallmatrix}1&1&0&0&1 \\ 1&0&0&0&0 \\ 0&1&0&1&0 \\ 0&1&1&0&0 \\ 1&0&0&0&1 \end{smallmatrix}\right]\]The number of paths of length 2 between each pair of vertices:
\[M^2=\left[\begin{smallmatrix}3&1&0&0&2 \\ 1&1&0&0&1 \\ 1&1&1&0&0 \\ 1&1&0&1&0 \\ 2&1&0&0&2\end{smallmatrix}\right]\]Euler and Hamilton Paths
Euler Paths and Circuits
An Euler path in G is a simple path containing every edge of G.


This is the recursive procedure to find the Euler path of a graph:
procedure FindEulerPath(V)
1. iterate through all the edges outgoing from vertex V;
remove this edge from the graph,
and call FindEulerPath from the second end of this edge;
2. add vertex V to the answer.The procedure could be rewrite in the non-recursive version:
stack St;
put start vertex in St;
until St is empty
let V be the value at the top of St;
if degree(V) = 0, then
add V to the answer;
remove V from the top of St;
otherwise
find any edge coming out of V;
remove it from the graph;
put the second end of this edge in St;Credit cp-algorithms for the pseudocode.
An Euler path in G is a simple path containing every edge of G.


This is the recursive procedure to find the Euler path of a graph:
procedure FindEulerPath(V)
1. iterate through all the edges outgoing from vertex V;
remove this edge from the graph,
and call FindEulerPath from the second end of this edge;
2. add vertex V to the answer.The procedure could be rewrite in the non-recursive version:
stack St;
put start vertex in St;
until St is empty
let V be the value at the top of St;
if degree(V) = 0, then
add V to the answer;
remove V from the top of St;
otherwise
find any edge coming out of V;
remove it from the graph;
put the second end of this edge in St;Credit cp-algorithms for the pseudocode.
Hamilton Paths and Circuits
That is, the simple path $x_0, x_1, \dots ,x_{n−1}, x_n$ in the graph $G = (V , E)$ is a Hamilton path if $V = {x_0, x_1, \cdots , x_{n−1}, x_n}$ and $x_i = x_j$ for $0 \le i < j \le n$, and the simple circuit $x_0, x_1, \dots , x_{n−1}, x_n, x_0$ (with $n > 0$) is a Hamilton circuit if $x_0, x_1, \dots , x_{n−1}, x_n$ is a Hamilton path.
There are no known simple necessary and sufficient criteria for the existence of Hamilton circuits. However, many theorems are known that give sufficient conditions for the existence of Hamilton circuits. Also, certain properties can be used to show that a graph has no Hamilton circuit.
