Introduction to Linear Algebra
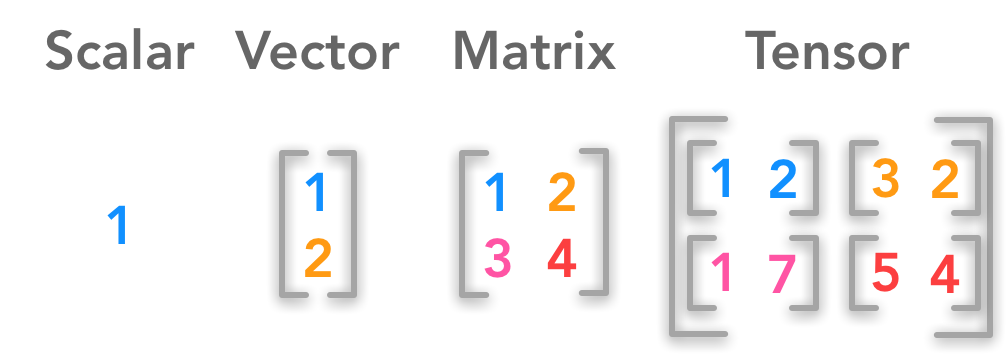
Vector
$$ x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} $$
Operations on Vectors
Vector-Vector addition & substraction
$$ x \pm y = \begin{bmatrix} x_1 \pm y_1 \\ x_2 \pm y_2 \\ \vdots \\ x_n \pm y_n \end{bmatrix} $$

Vector-Vector multiplication
$$ x * y = \begin{bmatrix} x_1 \times y_1 \\ x_2 \times y_2 \\ \vdots \\ x_n \times y_n \end{bmatrix} $$
For example:
\[\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} * \begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix} = \begin{bmatrix} 1 \times 4 \\ 2 \times 5 \\ 3 \times 6 \end{bmatrix} = \begin{bmatrix} 4 \\ 10 \\ 18 \end{bmatrix}\]For example:
\[\begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix} = [1 \times 4 +2 \times 5 + 3 \times 6] = 32\]$$ x y^T = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \begin{bmatrix} y_1 & y_2 & \dots & y_n \end{bmatrix} = \begin{bmatrix} x_1 y_1 & x_1 y_2 & \dots & x_1 y_n \\ x_2 y_1 & x_2 y_2 & \dots & x_2 y_b \\ \vdots & \vdots & \ddots & \vdots \\ x_m y_1 & x_m y_2 & \dots & x_m y_n \end{bmatrix} $$
For example:
\[\begin{bmatrix} 1 \\ 2 \\ 3\\ \end{bmatrix} \begin{bmatrix} 4 & 5 & 6 \end{bmatrix} = \begin{bmatrix} 1 \times 4 & 1 \times 5 & 1 \times 6 \\ 2 \times 4 & 2 \times 5 & 2 \times 6 \\ 3 \times 4 & 3 \times 5 & 3 \times 6 \\ \end{bmatrix} = \begin{bmatrix} 4 & 5 & 6 \\ 8 & 10 & 12 \\ 12 & 15 & 18 \end{bmatrix}\]Python code for vector multiplication:
>>> import numpy as np
>>> a = np.array([1], [2], [3])
>>> b = np.array([4,5,6])
>>> a*b
array([ 4, 10, 18])
>>> a.dot(b.T)
32
>>> np.outer(a,b)
array([[ 4, 5, 6],
[ 8, 10, 12],
[12, 15, 18]])
Matrices
For example $$ \begin{bmatrix} 23 & 402 \\ 69 & 221 \\ 118 & 0 \end{bmatrix} $$
Dimension of matrix is defined by number of rows $\times$ number of columns. In the above example, the dimension of matrix is 3 $\times$ 2.
Vector is a special case of matrix with dimension of (n $\times$ 1) in case of column vector or (1 $\times$ n) in case of row vector.
They use the notation $a_{ij}$ or $A_{ij}$ to denote the entry of A in the $i$th row and $j$th column.
\[A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{12} & \cdots & a_{1n} \end{bmatrix}\]Define a matrix in Python using numpy:
>>> import numpy as np
>>> m = np.array([[1, 2], [3, 4]])
>>> m
array([[1, 2],
[3, 4]])
Transpose
The transpose of a matrix $A \in \mathbb{R}^{m \times n}$ is $A^T \in \mathbb{R}^{m \times n}$ whose entries are given by
\[(A^T)_{ij} = A_{ji}\]The properties of transpose:
- $(A^T)^T=A$
- $(AB)^T = B^T A^T$
- $(A+B)^T = A^T + B^T$
Given a square matrix $A$, if $A = A^T$, A is said to be symmetric. It is anti-symmetric if $A = -A^T$. For any square matrix $A$, the matrix $A + A^T$ is symmetric and the matrix $A-A^T$ is anti-symmetric.
>>> m.T
array([[1, 3],
[2, 4]])
>>> m + m.T
array([[2, 5],
[5, 8]])
>>> m - m.T
array([[ 0, -1],
[ 1, 0]])
Identity Matrix
Python code for generating identity matrix:
>>> np.eye(2)
array([[1., 0.],
[0., 1.]])
>>> np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
Inverse
For example, let \(A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\). If $ad - bc \ne 0$, then A is invertible and
\[A^{-1} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\]Properties of inverse
- $(A^{-1})^{-1} = A$
- $(AB)^{-1} = B^{-1} A^{-1}$
- $(A^T)^{-1} = (A^{-1})^T$
The way to invert a matrix in Python:
>>> A = np.array([[1,2], [3,4]])
>>> np.invert(A)
array([[-2, -3],
[-4, -5]])
Matrices operations
Matrices addition/substraction
Matrix addition is the operation of adding two matrices by adding the corresponding entries together.
\[\begin{align} A \pm B & = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \pm \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \cdots & b_{mn} \\ \end{bmatrix} \\ & = \begin{bmatrix} a_{11} \pm b_{11} & a_{12} \pm b_{12} & \cdots & a_{1n} \pm b_{1n} \\ a_{21} \pm b_{21} & a_{22} \pm b_{22} & \cdots & a_{2n} \pm b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} \pm b_{m1} & b_{m2} \pm b_{m2} & \cdots & b_{mn} \pm b_{mn} \end{bmatrix} \end{align}\]Scalar multiplication
If $r$ is a scalar and A is a matrix, then scalar multiple $rA$ is the matrix whose elements are $r$ times the corresponding elements in $A$.
\[r \times A = r \times \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} = \begin{bmatrix} r \times a_{11} & r \times a_{12} & \cdots & r \times a_{1n} \\ r \times a_{21} & r \times a_{22} & \cdots & r \times a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ r \times a_{m1} & r \times a_{m2} & \cdots & r \times a_{mn} \end{bmatrix}\]For example:
\[3 \times \begin{bmatrix} 23 & 402 \\ 69 & 221 \\ 118 & 0 \end{bmatrix} = \begin{bmatrix} 69 & 1206 \\ 207 & 663 \\ 354 & 0 \end{bmatrix}\]In Python programming language:
>>> m = np.array([[23, 402], [69, 221], [118, 0]])
>>> 3*m
array([[ 69 1206]
[ 207 663]
[ 354 0]])
Matrix-Matrix multiplication
With two matrices $A \in \mathbb{R}^{m \times n}$ and $B \in \mathbb{R}^{n \times p}$, the product of A and B is the matrix $C \in \mathbb{R}^{m \times p}$ and \(C_{ij} = \sum^{n}_{k=1}A_{ik} B_{kj}\)
The product matrix only exists if the number of columns in $A$ equal to the number of rows in $B$.

Python demo code for matrix multiplication:
>>> A = np.array([[1,2], [3,4]])
>>> B = np.array([[5,6], [7,8]])
>>> A.dot(B)
array([[19, 22],
[43, 50]])
Properties of Matrix Multiplication: Given A be an $m \times n$ matrix, B and C have sizes for which the indicated sums and products are defined.
- $A(BC) = (AB)C$
- $A(B+C) = AB + AC$
- $(B+C)A = BA + CA$
- $r(AB) = (rA)B = A(rB)$ for any scalar r
- $I_m A = A I_n = A$
Read more:
Determinant
When the $(i,j)$-cofactor of A is the number $C_{ij}$ given by $$ C_{ij} = (-1)^{i+j} \det A_{ij} $$ the determinant of A can be defined by $$\begin{align} \det A &= a_{i1} C_{i1} + a_{i2} C_{i2} + \dots + a_{in} C_{in} \\ &= a_{1j} C_{1j} + a_{2j} C_{2j} + \dots + a_{nj} C_{nj} \end{align}$$
In the case $2 \times 2$ matrix:
\[\det \begin{bmatrix} a & b \\ c & b \end{bmatrix} = \begin{vmatrix} a & b \\ c & b \end{vmatrix} = ad - bc\]and $3 \times 3$ matrix:
\[\begin{align} \det \begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i \end{bmatrix} &= a \begin{vmatrix} e & f \\ h & i \end{vmatrix} - b \begin{vmatrix} d & f \\ g & i \end{vmatrix} + c \begin{vmatrix} d & e \\ g & h \end{vmatrix}\\ &= aei - afh -bdi +bfg + cdh - ceg \end{align}\]>>> import numpy as np
>>> A = np.array([[1,2], [3,4]])
>>> np.linalg.det(A)
-2.0000000000000004
Properties of the Determinant
- The determinant of the identity matrix is 1
\(\det I = \det \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = 1\) -
The determinant changes sign when two rows are exchanged
\(\begin{vmatrix} c & d \\ a & b \end{vmatrix} = - \begin{vmatrix} a & b \\ c & d \end{vmatrix}\) -
The determinant depends linearly on the first row
\(\begin{vmatrix} a+a' & b+b' \\ c & d \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} + \begin{vmatrix} a' & b' \\ c & d \end{vmatrix}\) \(\begin{vmatrix} ta & tb \\ c & d \end{vmatrix} = t \begin{vmatrix} a & b \\ c & d \end{vmatrix}\) -
If two rows of A are equal, then $\det A = 0$
\(\begin{vmatrix} a & b \\ a & b \end{vmatrix} = ab-ba = 0\) -
Substracting a multiple of one row from another row leaves the same determinant
\(\begin{vmatrix} a- tc & b - td \\ c & d \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} - t \begin{vmatrix} c & d \\ c & d \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix}\) -
If $A$ is triangular then $\det A$ is the product $a_{11} a_{22} \dots a_{nn}$ of the diagonal entries.
If the triangular A has 1s , then $\det A = 1$
\(\begin{vmatrix} a & b \\ 0 & d \end{vmatrix} = \begin{vmatrix} a & 0 \\ c & d \end{vmatrix} = ad\) -
If $A$ is singular, then $\det A = 0$. If $A$ is invertible, then $\det A \ne 0$
-
The determinant of AB is the product of $\det A$ times $\det B$: \(|A| |B| = |AB|\)
The special case is when $B = A^{-1}$:
\((\det A) (\det A^{-1}) = \det AA^{-1} = \det I = 1\) \(\Rightarrow \det A^{-1} = \frac{1}{\det A}\) - The transpose of $A$ has the same determinant as $A$ itself: $\det A^T = \det A$
\(|A| = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = \begin{vmatrix} a & c \\ b & d \end{vmatrix} = |A^T|\)
Application of Determinants
-
Computation of $A^{-1}$:
\[A^{-1} = \frac{C^T}{\det A} \text{ or } (A^{-1})_{ij} = \frac{C_{ij}}{\det A}\]In case of 2 by 2 matrix, we have \(\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} = \frac{1}{\det A} \begin{bmatrix} C_{11} & C_{21} \\ C_{12} & C_{22} \end{bmatrix} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\)
-
The Solution of $Ax = b$ (Cramer’s rule)
\[x_j = \frac{\det B_j}{\det A} \text{, where } B_j = \begin{bmatrix} a_{11} & a_{12} & b_1 & a_{1n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{n1} & a_{n2} & b_n & a_{nn} \\ \end{bmatrix} \text{ has b in column j}\] -
Determinants as Area or Volume
If $A$ is a $2 \times 2$ matrix, the area of the parallelogram determined by te columns of $A$ is $|\det A|$. If $A$ is a $3 \times 3$ matrix, the volume of the paralellepiped determined by the columns of $A$ is $|\det A|$.
Linear Independence and Rank
An set of vectors $\{ v_1, \dots , v_p \} \in \mathbb{R}^n$ is said to be linearly independent if the vector equation $$ x_1 v_1 + x_2 v_2 + \dots + x_p v_p = 0 $$ has only the trivial solution.
The set $\{ v_1, \dots , v_p \} $ is said to be linearly dependent if there exist weights $c_1, \dots , c_p$, not all zero, such that $$ c_1 v_1 + c_2 v_2 + \dots + c_p v_p = 0 $$
Given a matrix $A \in \mathbb{R}^{m \times n}$:
- If the column rank of $A$ is equal to its row rank, this number is the rank of $A$.
The properties of the rank, for $A, B \in \mathbb{R}^{m\times n}$:
- $rank(A) \le \min (m,n)$. If $rank(A) = \min(m,n)$, $A$ is said to be full rank.
- $rank(A) = rank(A^T)$
- $rank(AB) \le \min(rank(A), rank(B)$
- $rank(A+B) \le rank(A) + rank(B)$
Norms
- Nonnegativity and mapping of the identity: if $x \ne 0$, then $\|x\| > 0$, and $\| 0 \|=0$
- Scalar multiplication: $\| ax \| = |a| \| x\|$, for all real $a$
- Triangle inequality: $\| x+y \| \le \|x\| + \|y\|$
For $p \ge 1$, $L _ p$ norm is defined by \(\| x \| _ {p} = \left( \sum_i \| x_i \|^p \right)^{\frac{1}{p}}\)
Some common $L_p$ norms:
- $ | x |_ 1 = \sum _ {i} |x_i|$, also called the Manhattan norm.
- $| x |_ 2 = \sqrt{\sum _ {i} x_i^2}$, also called the Euclidean norm, the Euclidean length, or the length of the vector. The $L_2$ is the square root of the inner product of the vector with itself: $|x|_ 2 = \sqrt{\langle x,x \rangle}$.
- $| x |_ \infty = \max_{i} |x_i|$, also called the max norm or the Chebyshev norm.
A generalization of $L_p$ is the weighted $L_p$ norm: \(\| x \|_ {wp} = \left(\sum_{i} w_i |x_i|^p \right)^{\frac{1}{p}}\)
Quadratic forms
Positive definite and Positive semidefinite
- A is positive definite if for all nonzero vectors $x\in \mathbb{R}^n$, $x^T Ax > 0$.
- A is positive semidefinite if for all nonzero vectors $x\in \mathbb{R}^n$, $x^T Ax \ge 0$.
- A is negative definite if for all nonzero vectors $x\in \mathbb{R}^n$, $x^T Ax < 0$.
- A is negative semidefinite if for all nonzero vectors $x\in \mathbb{R}^n$, $x^T Ax \le 0$.
- A is indefinite if A is neither positive semidefinite or negative semidefinite.
Eigenvalues and Eigenvectors
How to find Eigenvalues and Eigenvectors?
-
Find the values of $\lambda$ which satisfy the characteristic equation:
\[\det (A- \lambda I) = 0\]where $I$ is the identity matrix.
The solution of this equation is the eigenvalue of the matrix.
-
For each eigenvalue solved, we have
\[(A - \lambda I) x = 0\]where x is the eigenvector associated with eigenvalue $\lambda$.
Find X by Gaussian elimination.
For example, find the eigenvalues and eigenvectors of \(A= \begin{bmatrix} 2 & -4 \\ -1 & -1 \end{bmatrix}\)
-
Solve the characteristic equation for eigenvalues:
\[\begin{align} \det (A - \lambda I) &= \det \begin{bmatrix} 2 - \lambda & -4 \\ -1 & -1 - \lambda \end{bmatrix} \\ & = (2 - \lambda)(-1-\lambda) - (-4)(-1) \\ &= \lambda^2 -\lambda - 6 \\ &= (\lambda -3)(\lambda + 2) \\ \end{align}\]So that
\[\begin{align} \det (A - \lambda I) &= 0 \\ \Leftrightarrow (\lambda -3)(\lambda + 2) &= 0 \\ \Leftrightarrow \lambda &= 3 \\ \text{ or } \lambda &= -2 \end{align}\]The eigenvalues of A are $\lambda = 3 \text{ or } \lambda = -2 $
-
Solve for eigenvectors $x = \begin{bmatrix} x_1 \ x_2 \end{bmatrix}$:
\[(A-3I)x = 0\]-
For $\lambda = 3$, we have the augmented matrix:
\[\begin{bmatrix} 2-3 & -4 & 0 \\ -1 & -1 - 3 & 0 \end{bmatrix} \rightarrow \begin{bmatrix} -1 & -4 & 0 \\ -1 & -4 & 0 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 4 & 0 \\ 0 & 0 & 0 \end{bmatrix}\]The eigenvector corresponding to $\lambda = 3$:
\(x = k \begin{pmatrix} -4 \\ 1 \end{pmatrix}\) where $k$ is nonzero scalar.
-
For $\lambda = -2$, the eigenvectors have the form:
\(x = k\begin{pmatrix} 1\\ 1 \end{pmatrix}\) where k is nonzero scalar.
-
The numpy package in Python supports finding eigenvalues quickly:
>>> import numpy as np
>>> A = np.array([[2, -4],[-1,-1]])
>>> np.linalg.eigvals(A)
array([ 3., -2.])
Reference
[1] Lecture from course Machine learning at VEF Academy.
[2] Zico Kolter. Linear algebra review and reference, 2008.
[3] D.C. Lay, S.R. Lay, and J.J. McDonald. Linear Algebra and Its Applications. Pearson Education, 2015.
[4] G. Strang. Linear Algebra and Its Applications. Thomson, Brooks/Cole, 2006.